Filters
Question type
Correct Answer

verified
Correct Answer
verified
Question 22
Multiple Choice
A pond initially contains 70,000 gallons of water and an unknown amount of pesticide. Water containing 0.05 grams of pesticide per gallon flows into the pond at a rate of 300 gallons per hour. The mixture flows out of the pond at the same rate, so the amount of water in the pond remains constant. Assume the pesticide is uniformly mixed throughout the pond.Which of these is the general solution of the differential equation for the amount of pesticide, P(t) , in the pond at any time t?
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) A) and D)
F) B) and C)
F) B) and C)
Correct Answer

verified
Correct Answer
verified
Question 23
Short Answer
An antibiotic is being administered intravenously to a patient. Fluid containing 8.0 mg/Cm3 of the antibiotic enters the patient's bloodstream at a rate of 100 Cm3/hour. The antibiotic is absorbed by the body or otherwise leaves the bloodstream at a rate proportional to the amount present, with a rate constant of 0.6 per hour. Assume the antibiotic is always uniformly distributed throughout the bloodstream.How much of the antibiotic is present in the bloodstream after a very long time? Round your answer to the nearest hundredth of a milligram.
Correct Answer

verified
Correct Answer
verified
Question 24
Multiple Choice
Newton's Law of Cooling states that the temperature of an object changes at a rate proportional to the difference between the temperature of the object itself and the temperature of its surroundings (typically the ambient temperature) . Suppose the ambient temperature is 72°F and the rate constant is 0.1 per minute.Suppose the temperature of the object is initially 107°F. What is the solution to the initial-value problem comprised of the differential equation for the temperature of the object, T(t) , at any time t and the initial condition T(0) = 107?
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
F) None of the above
G) B) and C)
G) B) and C)
Correct Answer

verified
Correct Answer
verified
Question 25
Multiple Choice
Which of the following pairs of values of A and B are such that all solutions of the differential equation 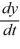 = Ay + B diverge away from the line y = 10 as t ? Select all that apply.
= Ay + B diverge away from the line y = 10 as t ? Select all that apply.
A) A = -2, B = 20
B) A = 3, B = -30
C) A = 1, B = -10
D) A = -1, B = 10
E) A = -2, B = -20
F) A = 10, B = -1
G) A = 2, B = -20
H) C) and E)
I) A) and E)
I) A) and E)
Correct Answer

verified
Correct Answer
verified
Question 26
Short Answer
Newton's Law of Cooling states that the temperature of an object changes at a rate proportional to the difference between the temperature of the object itself and the temperature of its surroundings (typically the ambient temperature). Suppose the ambient temperature is 72°F and the rate constant is 0.12 per minute.Suppose the temperature of the object is initially 97°F. Given the initial condition T(0) = 97, how many minutes does it take the object to reach a temperature of 80.3°F? Round your answer to the nearest tenth of a minute.
Correct Answer

verified
Correct Answer
verified
Question 27
Essay
For each of the following ordinary differential equations, identify the order and indicate whether it is linear or nonlinear.
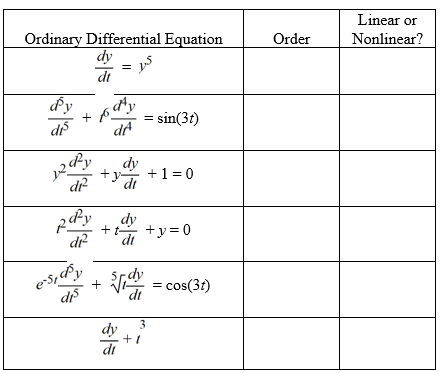
Correct Answer

verified
Correct Answer
verified
Question 28
Essay
Eight differential equations and four slope fields are given below.
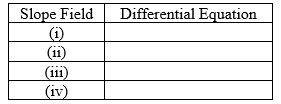
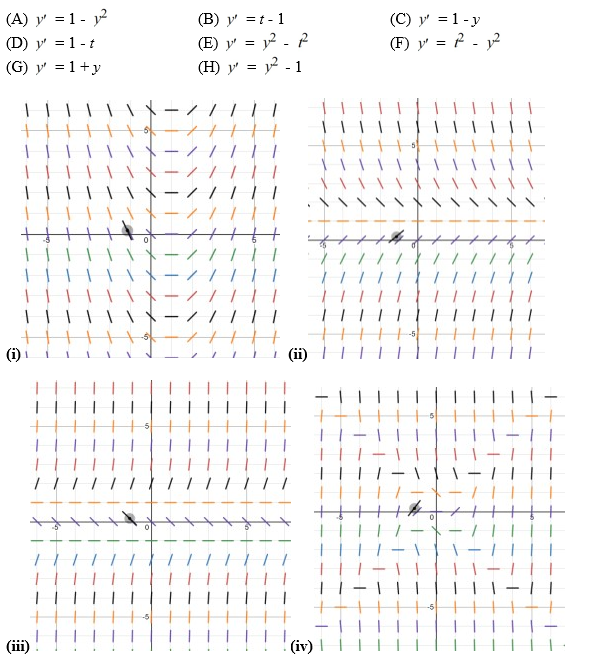 Determine the differential equation that corresponds to each slope field. Fill in the correct letter next to each number below:
Determine the differential equation that corresponds to each slope field. Fill in the correct letter next to each number below:
Correct Answer

verified
Correct Answer
verified
Showing 21 - 28 of 28
Related Exams